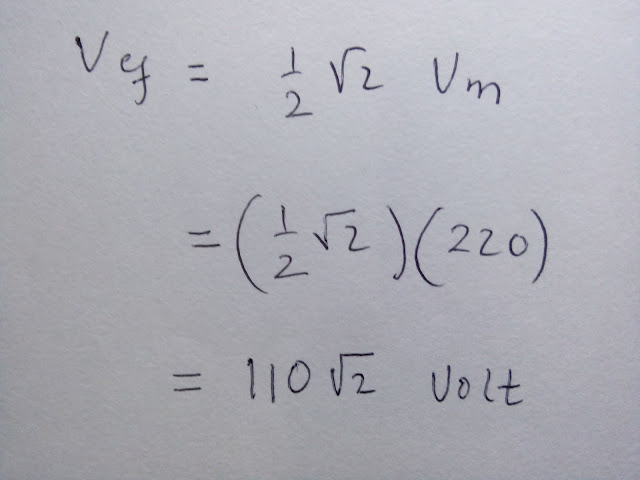Soal Jawab Listrik Arus Bolak-Balik Standar UAS SMA / SMK / MA
Pada kesempatan kali ini, Ilmu Fisika akan membahas Soal Jawab Listrik Arus Bolak-Balik Standar UAS SMA / SMK / MA.
Tegangan dan Arus Sesaat
Rumusan Umum Tegangan Sesaat adalah
$\displaystyle V_{t}=V_{m}sin\,\theta$
$\displaystyle V_{t}=V_{m}sin\,\omega t$
$\displaystyle V_{t}=V_{m}sin\,2\pi \,f\, t$
$\displaystyle V_{t}=V_{m}sin\,\frac{2\pi}{T} \, t$
Rumusan Umum Arus Sesaat adalah
$\displaystyle I_{t}=I_{m}sin\,\theta$
$\displaystyle I_{t}=I_{m}sin\,\omega t$
$\displaystyle I_{t}=I_{m}sin\,2\pi \,f\, t$
$\displaystyle I_{t}=I_{m}sin\,\frac{2\pi}{T} \, t$
Tegangan / Arus Bolak-Balik Efektif
Suatu sumber tegangan bolak - balik memiliki nilai maksimum $220$ $V$. Nilai tegangan efektifnya adalah ... $V$.
Rumusan hubungan tegangan maksimum dengan tegangan efektif adalah \[V_{ef}=\frac{1}{2}\sqrt{2}\,V_{m}\]
Tegangan / Arus Rata-Rata
Suatu sumber tegangan bolak - balik memiliki nilai maksimum $220$ $V$. Nilai tegangan rata-ratanya adalah ... $V$.
Rumusan hubungan tegangan maksimum dengan tegangan efektif adalah \[\bar{V}
=\frac{2}{\pi}\,V_{m}\]
$\bar{V}=\displaystyle \frac{2}{\frac{22}{7}}\,220$ = $140\,V$
Reaktansi Induktif
Rumusan dasarnya adalah \[X_{L}=\omega \,L\] \[X_{L}=2\,\pi \,f \,L\]
Suatu kapasitor memiliki kapasitas,$C$ = $1000\,µF$, dialiri arus listrik AC dengan frekuensi, $f$ = $50\,Hz$, maka reaktansi kapasitifnya adalah ... Ω.
Dari rumusan $X_{L}=X_{C}$, diperoleh :
Materi Medan Magnet Induksi yang akan dibahas antara lain tentang :
- Arus dan Tegangan Maksimum
- Arus dan Tegangan Sesaat
- Arus dan Tegangan Efektif
- Arus dan Tegangan Rata-rata
- Reaktansi Induktif, Reaktansi Kapasitif
- Frekuensi Resonansi
Tegangan dan Arus Sesaat
Rumusan Umum Tegangan Sesaat adalah
$\displaystyle V_{t}=V_{m}sin\,\theta$
$\displaystyle V_{t}=V_{m}sin\,\omega t$
$\displaystyle V_{t}=V_{m}sin\,2\pi \,f\, t$
$\displaystyle V_{t}=V_{m}sin\,\frac{2\pi}{T} \, t$
Rumusan Umum Arus Sesaat adalah
$\displaystyle I_{t}=I_{m}sin\,\theta$
$\displaystyle I_{t}=I_{m}sin\,\omega t$
$\displaystyle I_{t}=I_{m}sin\,2\pi \,f\, t$
$\displaystyle I_{t}=I_{m}sin\,\frac{2\pi}{T} \, t$
Tentukan besarnya Tegangan sesaat, $V_{t}$, apabila sudut fase adalah $30⁰$ dari suatu sumber Tegangan dengan tegangan maksimumnya $220$ $V$ !
Penyelesaian :
Sudut fase, $\theta$ = $30⁰$
Tegangan maksimum, $V_{m}$ = $220$ $V$
Maka
$\displaystyle V_{t}=V_{m}sin\,\theta$
$\displaystyle V_{t}=\,220\,sin\,30⁰$
$\displaystyle V_{t}=\,110\,V$
Sudut fase, $\theta$ = $30⁰$
Tegangan maksimum, $V_{m}$ = $220$ $V$
Maka
$\displaystyle V_{t}=V_{m}sin\,\theta$
$\displaystyle V_{t}=\,220\,sin\,30⁰$
$\displaystyle V_{t}=\,110\,V$
Tegangan / Arus Bolak-Balik Efektif
Suatu sumber tegangan bolak - balik memiliki nilai maksimum $220$ $V$. Nilai tegangan efektifnya adalah ... $V$.
Penyelesaian :
Tegangan maksimum, $V_{m}$ = $220$ $V$
Rumusan hubungan tegangan maksimum dengan tegangan efektif adalah \[V_{ef}=\frac{1}{2}\sqrt{2}\,V_{m}\]
Diperoleh
$V_{ef}=\displaystyle \frac{1}{2}\sqrt{2}\,220$
$V_{ef}=\displaystyle 110\sqrt{2}\,V\simeq 155\,V$
Tegangan / Arus Rata-Rata
Suatu sumber tegangan bolak - balik memiliki nilai maksimum $220$ $V$. Nilai tegangan rata-ratanya adalah ... $V$.
Penyelesaian :
Tegangan maksimum, $V_{m}$ = $220$ $V$
Rumusan hubungan tegangan maksimum dengan tegangan efektif adalah \[\bar{V}
=\frac{2}{\pi}\,V_{m}\]
Diperoleh
$\bar{V}=\displaystyle \frac{2}{\pi}\,220$
Reaktansi Induktif
Rumusan dasarnya adalah \[X_{L}=\omega \,L\] \[X_{L}=2\,\pi \,f \,L\]
Suatu induktor memiliki induktansi diri, $L$ = $200\,mH$, dialiri arus listrik AC dengan frekuensi,$f$ = $50\,Hz$, maka reaktansi induktifnya adalah ... $Ω$.
Penyelesaian :
$L$ = $200\,mH$ = $2\,x\,10^{-3}\,H$
$f$ = $50\,Hz$
Maka,
$\displaystyle X_{L}=(2\pi )(50)(2x10^{-3})=0,2\pi \,\Omega$
Reaktansi Kapasitif
Rumusan dasarnya adalah \[X_{C}=\displaystyle \frac{1}{\omega \,C}\] \[X_{C}=\displaystyle \frac{1}{2\,\pi \,f\,C}\]
Penyelesaian :
$L$ = $200\,mH$ = $2\,x\,10^{-3}\,H$
$f$ = $50\,Hz$
Maka,
$\displaystyle X_{L}=(2\pi )(50)(2x10^{-3})=0,2\pi \,\Omega$
Reaktansi Kapasitif
Rumusan dasarnya adalah \[X_{C}=\displaystyle \frac{1}{\omega \,C}\] \[X_{C}=\displaystyle \frac{1}{2\,\pi \,f\,C}\]
Suatu kapasitor memiliki kapasitas,$C$ = $1000\,µF$, dialiri arus listrik AC dengan frekuensi, $f$ = $50\,Hz$, maka reaktansi kapasitifnya adalah ... Ω.
Penyelesaian :
$C$ = $1000\,µF$ = $1000\,x\,10^{-6}\,F$ = $10^{-3}\,F$
$f$ = $50\,Hz$
Maka,
$\displaystyle X_{C}=\frac{1}{(2\pi)(50)(10^{-3})}=\frac{10}{\pi }\,\Omega$
Frekuensi Resonansi
Frekuensi resonansi terjadi bila \[X_{L}=X_{C}\]
Suatu perangkat radio memiliki induktor dengan induktansi diri, $L$ = $100\,H$ dan kapasitas kapasitor, $C$ = $1\,µF$. Maka perangkat radio tersebut menerima frekuensi resonansi sebesar ... $Hz$.
Maka,
$\displaystyle X_{C}=\frac{1}{(2\pi)(50)(10^{-3})}=\frac{10}{\pi }\,\Omega$
Frekuensi Resonansi
Frekuensi resonansi terjadi bila \[X_{L}=X_{C}\]
Suatu perangkat radio memiliki induktor dengan induktansi diri, $L$ = $100\,H$ dan kapasitas kapasitor, $C$ = $1\,µF$. Maka perangkat radio tersebut menerima frekuensi resonansi sebesar ... $Hz$.
Penyelesaian :
$L$ = $100\,H$ = $10^{2}\,H$
$C$ = $1\,µF$ = $10^{-6}\,F$
Dari rumusan $X_{L}=X_{C}$, diperoleh :
$\displaystyle \omega \,L=\frac{1}{\omega \,C}$
$\displaystyle 2\pi f_{0}L=\frac{1}{2\pi f_{0}C}$
$\displaystyle f_{0}=\frac{1}{2\pi }\sqrt{\frac{1}{LC}}$
$\displaystyle f_{0}=\frac{1}{2\pi }\sqrt{\frac{1}{(10^{2})(10^{-6})}}=\frac{50}{\pi }\,Hz$