Contoh Soal dan Pembahasan Gelombang Mekanik
Lanjutan dari Gelombang Mekanik Beserta Pengelompokan dan Perumusannya
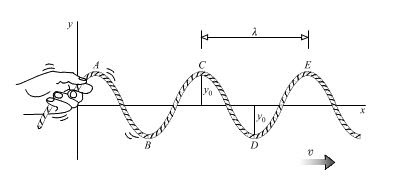
Ujung seutas tali yang panjang digetarkan vertikal seperti yang ditunjukkan pada ilustrasi di atas. Getaran tersebut menghasilkan $gelombang$ $berjalan$. Gelombang ini berjalan dari titik tangkap antara sumbu y dan sumbu x (titik origin) menuju ke arah sumbu x positif.
Dengan kata lain, suatu gelombang ditimbulkan pada tali degan getaran sinusoida dari tangan ke ujung tali. Sinusoida adalah istilah bentuk gelombang yang menyerupai grafik fungsi sinus. Semoga sudah ingat ya, pembahasan mengenai Trigonometri di pelajaran Matematika.
Mari kita simak lagi pembahasan sebelumya, Teori Gelombang Mekanik, energi dibawa oleh gelombang dari sumber ke kanan, di sepanjang tali. Arah transportasi energi ini disebut arah perambatan gelombang.
Setiap partikel pada tali, misalnya benda di titik C, bergerak naik turun, tegak lurus terhadap arah atau garis perambatan. Gelombang yang memiliki getaran tegak lurus dengan arah perambatan disebut gelombang transversal.
Baik, sekarang mari kita belajar tentang persamaan umum gelombang berjalan.
Simpangan getar untuk titik asal pada gambar di atas akan mengikuti persamaan simpangan harmonik sederhana, yaitu:
\[y=Asin\theta\]
\[y=Asin(\omega t)\]
\[y=Asin(2\pi \frac{t}{T})\]
\[y=Asin(2\pi \phi)\]
Dengan
\[\phi=\frac{t}{T}\]
Merupakan $fase$ $gelombang$ dan $\theta$ = $2\pi \phi$ merupakan $sudut$ $fase$.
Gelombang merambat dari titik asal $O$ ke arah sumbu $x$ positif. Suatu titik $P$ misalnya, yang terletak sejauh $x$ di sebelah kanan titik $O$ kan ikut bergetar beberapa saat kemudian setelah gelombang yang merambat dari titik $O$ mencapai titik $P$.
Waktu yang diperlukan oleh gelombang berjalan untuk merambat dari titik $O$ ke titik $P$ adalah $x/v$ sekon. Jadi, jika $O$ telah bergetar selama $t$ sekon, titik $P$ baru bergetar selama $t_{P}$ = $(t-\frac{x}{v})$ sekon, sehingga persamaan simpangan gelombangnya di titik $P$ adalah
\[y_{P}=Asin(\omega(t-\frac{x}{v}))\]
\[y_{P}=Asin(2\pi ft-2\pi f\frac{x}{v})\]
\[y_{P}=Asin(\frac{2\pi }{T}t-\frac{2\pi }{\lambda}x)\]
\[y_{P}=Asin(\omega t-kx)\]
Rumus – rumus di atas disebut sebagai persamaan gelombang berjalan, mengandung banyak besarn, yaitu simpangan, amplitudo, frekuensi sudut, frekuensi linear, periode gelombang, bilangan gelombang, dan cepat rambat gelombang, dengan ketentuan sebagai berikut:
Referensi [2] Selengkapnya »
Ujung seutas tali yang panjang digetarkan vertikal seperti yang ditunjukkan pada ilustrasi di atas. Getaran tersebut menghasilkan $gelombang$ $berjalan$. Gelombang ini berjalan dari titik tangkap antara sumbu y dan sumbu x (titik origin) menuju ke arah sumbu x positif.
Dengan kata lain, suatu gelombang ditimbulkan pada tali degan getaran sinusoida dari tangan ke ujung tali. Sinusoida adalah istilah bentuk gelombang yang menyerupai grafik fungsi sinus. Semoga sudah ingat ya, pembahasan mengenai Trigonometri di pelajaran Matematika.
Mari kita simak lagi pembahasan sebelumya, Teori Gelombang Mekanik, energi dibawa oleh gelombang dari sumber ke kanan, di sepanjang tali. Arah transportasi energi ini disebut arah perambatan gelombang.
Setiap partikel pada tali, misalnya benda di titik C, bergerak naik turun, tegak lurus terhadap arah atau garis perambatan. Gelombang yang memiliki getaran tegak lurus dengan arah perambatan disebut gelombang transversal.
Baik, sekarang mari kita belajar tentang persamaan umum gelombang berjalan.
Simpangan getar untuk titik asal pada gambar di atas akan mengikuti persamaan simpangan harmonik sederhana, yaitu:
\[y=Asin\theta\]
\[y=Asin(\omega t)\]
\[y=Asin(2\pi \frac{t}{T})\]
\[y=Asin(2\pi \phi)\]
Dengan
\[\phi=\frac{t}{T}\]
Merupakan $fase$ $gelombang$ dan $\theta$ = $2\pi \phi$ merupakan $sudut$ $fase$.
Gelombang merambat dari titik asal $O$ ke arah sumbu $x$ positif. Suatu titik $P$ misalnya, yang terletak sejauh $x$ di sebelah kanan titik $O$ kan ikut bergetar beberapa saat kemudian setelah gelombang yang merambat dari titik $O$ mencapai titik $P$.
Waktu yang diperlukan oleh gelombang berjalan untuk merambat dari titik $O$ ke titik $P$ adalah $x/v$ sekon. Jadi, jika $O$ telah bergetar selama $t$ sekon, titik $P$ baru bergetar selama $t_{P}$ = $(t-\frac{x}{v})$ sekon, sehingga persamaan simpangan gelombangnya di titik $P$ adalah
\[y_{P}=Asin(\omega(t-\frac{x}{v}))\]
\[y_{P}=Asin(2\pi ft-2\pi f\frac{x}{v})\]
\[y_{P}=Asin(\frac{2\pi }{T}t-\frac{2\pi }{\lambda}x)\]
\[y_{P}=Asin(\omega t-kx)\]
Rumus – rumus di atas disebut sebagai persamaan gelombang berjalan, mengandung banyak besarn, yaitu simpangan, amplitudo, frekuensi sudut, frekuensi linear, periode gelombang, bilangan gelombang, dan cepat rambat gelombang, dengan ketentuan sebagai berikut:
- Jika semula titik asal $O$ digetarkan ke atas, maka amplitudo bernilai positif, sebaliknya jika bergetar ke bawah dulu maka amplitudo bernilai negatif
- Jika arah rambat gelombang ke kanan, tanda koefisien $x$ dan $t$ berbeda, yaitu jika $t$ bertanda positif, maka $x$ bertanda negatif. Dan jika arah rambat gelombang ke kiri, tanda koefisien $x$ dan $t$ sama
Contoh : Dari persamaan gelombang berikut, $y=2sin\pi(5t-2x)$ tentukan nilai-nilai: amplitudo, frekuensi sudut, frekuensi linear, periode gelombang, bilangan gelombang, dan cepat rambat gelombang, $t$ dalam sekon, $x$ dalam meter
PembahasanDari persamaan gelombang \[y_{P}=Asin(\frac{2\pi }{T}t-\frac{2\pi }{\lambda}x)\] dan modifikasi soal menjadi \[y_{P}=2sin(5\pi t-2\pi x)\]
Diperoleh hubungan:
$A$ = 2 meter
$\omega$ = $5\pi$
Maka
$\omega$ = $5\pi$ setara dengan $\omega$ = $2\pi f$
Sehingga, $f$ = $\frac{5\pi}{2\pi}$ = 2,5 Hz
Dan $T$ = $\frac{1}{f}$ = $\frac{1}{2,5}$ = 0,4 sekon
Kemudian, $k$ = $2\pi$
Untuk mendapatkan nilai $\lambda$, persamaan tadi disetarakan dengan $k$ = $\frac{2\pi}{\lambda}$
Diperoleh $\lambda$ = 1 meter
Nilai cepat rambat diperoleh dari persamaan \[\nu=\frac{\lambda}{T}\]
Diperoleh \[\nu=2,5\frac{m}{s}\]
Diperoleh hubungan:
$A$ = 2 meter
$\omega$ = $5\pi$
Maka
$\omega$ = $5\pi$ setara dengan $\omega$ = $2\pi f$
Sehingga, $f$ = $\frac{5\pi}{2\pi}$ = 2,5 Hz
Dan $T$ = $\frac{1}{f}$ = $\frac{1}{2,5}$ = 0,4 sekon
Kemudian, $k$ = $2\pi$
Untuk mendapatkan nilai $\lambda$, persamaan tadi disetarakan dengan $k$ = $\frac{2\pi}{\lambda}$
Diperoleh $\lambda$ = 1 meter
Nilai cepat rambat diperoleh dari persamaan \[\nu=\frac{\lambda}{T}\]
Diperoleh \[\nu=2,5\frac{m}{s}\]
Referensi [2] Selengkapnya »
