Alat Optik - Mata, Lup, Mikroskop, Teropong
Mata
Mata adalah alat optik alami. Mata terdiri dari kornea, iris, pupil, lensa, retina. Kornea berfungsi sebagai lapisan pelindung. Iris membentuk celah lingkaran yang disebut pupil. Iris mengatur lebar pupil, untuk mengatur banyaknya cahaya yang masuk ke mata. Di tempat yang terang, pupil mengecil supaya lebih sedikit cahaya yang masuk ke mata sehingga mata tidak silau, sedangkan di tempat yang gelap, pupil membesar supaya lebih banyak cahaya yang masuk ke mata.
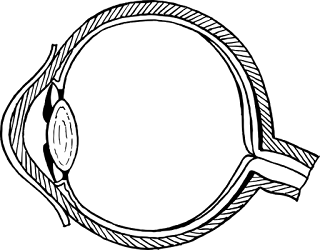Oleh lensa mata, cahaya yang masuk diteruskan ke retina yang tersusun atas jutaan sel ayng sangat peka terhadap rangsang. Rangsangan berupa cahaya yang diterima oleh retina ini akhirnya diubah menjadi sinyal-sinyal yang oleh sistem syaraf kita dikirim ke otak. Di otak ini lah sinyal-sinyal tersebut diterjemahkan, misalnya sinyal dari cahaya yang dipancarkan oleh sebuah laptop diterjemahkan sebagai "kita melihat sebuah laptop".Bayangan dari suatu benda yang terbentuk di retina disebabkan oleh efek pembiasan ayng terjadi pada pupil dan lensa karena indeks bias kornea, pupil, lensa mata dan cairan mata nyaris sama besar. Agar sebuah benda dapat terlihat jelas, bayangan benda harus terbentuk di retina., yaitu bersiat nyata, terbalik dan diperkecil. Agar bayangan selalu tepat di retina, pajang fokus lensa harus dapat berubah-ubah sesuai dengan jarak benda yang dilihat, diatur oleh otot siliar.
Ketika melihat benda-benda jauh, otot siliar mengendur sehingga lensa mata lebih pipih, dikatakan mata dalam keadaan tak berakomodasi. Sebaliknya, ketika melihat benda-benda yang dekat, otot siliar menegang sehingga mata lebih cembung, dikatakan mata dalam kondisi berakomodasi. Kemampuan berubahnya kelengkungan lensa mata ini disebut Daya Akomodasi.
Jangkauan penglihatan mata dalam keadaan tidak berakomodasi disebut titik jauh atau punctum remotum (PR). Untuk mata normal, titik jauh berada pada jarak tak hingga (PR = ~).
Jangkauan penglihatan mata dalam keadaan berakomodasi maksimum disebut titik dekat atau punctum proximum (PP) atau $S_{n}$. Untuk mata normal, titik dekat berkisar 25 cm.
Cacat mata, pada kali ini ada dua yang akan dibahas, yaitu rabun jauh dan rabun dekat. Rabun jauh adalah cacat mata tidak mampu melihat jelas benda-benda yang jauh. Kemampuan memipihnya mata sudah berkurang. Titik jauhnya terhingga (PR < ~ ). Sebaliknya, rabun dekat adalah cacat mata tidak mampu melihat benda-benda yang dekat. Kemampuan menebalnya mata sudah berkurang.
Pada rabun jauh, bayangan yang terbentuk lensa mata di depan retina, sehingga agar bayangan jatuh tepat di retina, mata perlu bantuan lensa divergen (lensa cekung). Kacamata divergen membantu membentuk bayangan di titik jauh mata, kemudian lensa mata membentuk bayangan akhir di retina. Jadi untuk kacamata berlaku $s'$ = $- PR$ .
Oleh karena benda berada di jauh tak hingga ( $s$ = ~ ), maka kuat lensa yang diperlukan untuk mata miopi (rabun jauh) dapat dihitung sebagai berikut: \[\frac{1}{f}=\frac{1}{s}+\frac{1}{s'},\,atau,\,\,\,P=\frac{1}{\infty{}}+\frac{1}{-PR}=-\frac{1}{PR}\]
Apabila titik jauh miopi, $PR$ dalam $cm$, dan kuat lensa, $P$ dalam dipotri, maka \[P=-\frac{100}{PR}\]
Contoh soal rabun jauh
Seorang penderita rabun jauh (miopi) mempunyai titik jauh 75 cm di depan mata. Tentukan kuat lensa dan fokus lensa kacamata yang harus dipakai agar orang itu dapat melihat dengan jelas benda yang sangat jauh !
Pembahasan
Data yang diperoleh adalah $PR$ = 75 cm. Dengan menggunakan persamaan untuk mata rabun jauh diperoleh \[P=\frac{-100}{PR}=\frac{-100}{75}=\frac{-4}{3}\,\,Dioptri\]
LUP (Kaca Pembesar)Seorang penderita rabun jauh (miopi) mempunyai titik jauh 75 cm di depan mata. Tentukan kuat lensa dan fokus lensa kacamata yang harus dipakai agar orang itu dapat melihat dengan jelas benda yang sangat jauh !
Pembahasan
Data yang diperoleh adalah $PR$ = 75 cm. Dengan menggunakan persamaan untuk mata rabun jauh diperoleh \[P=\frac{-100}{PR}=\frac{-100}{75}=\frac{-4}{3}\,\,Dioptri\]
fokus lensa yang digunakan adalah \[f=\frac{1}{P}=\frac{1}{-4/3}=\frac{-3}{4}\,cm\]
Tanda minus menunjukkan bahwa lensa yang digunakan bersifat divergen.
Pada rabun dekat (hipermetropi), bayangan jatuh melebihi retina, maka agar bayangan tepat di retina, penderita rabun dekat perlu bantuan lensa konvergen (cembung). Kacamata konvergen membantu membentuk bayangan di retina. Titik dekat mata hipermetropi lebih besar dari 25 cm, akibatnya penderita hipermetropi dapat melihat benda-benda yang jauh tapi tidak dapat melihat dengan jelas benda-benda yang dekat (jaraknya lebih kecil dari titik dekat matanya). Dengan kata lain, kacamata membentuk bayangan di titik dekat mata, kemudian lensa mata membentuk bayangan akhir di retina. Jadi untuk kacamata hipermetropi berlaku \[s'=-PP=-S_{n}\]
Rumusan mencari kekuatan lensa : \[P=\frac{1}{f}=\frac{1}{s}+\frac{1}{s'}=\frac{1}{s}-\frac{1}{S_{n}}\]
Jika $s$, jarak benda dikehendaki dapat terlihat pada jarak normal, yaitu 25 cm, maka \[P=\frac{1}{f}=\frac{1}{0,25}-\frac{1}{S_{n}}=4-\frac{1}{S_{n}}\]
dalam hal ini, satuan panjang dalam meter. Apabila menggunakan $cm$, persamaannya menjadi \[P=\frac{1}{f}==4-\frac{100}{S_{n}}\]
Contoh soal rabun dekat
Titik dekat seseorang yang rabun dekat adalah 2 meter. Tentukanlah kuat lensa kacamata yang diperlukan jika orang tersebut ingin membaca dengan jelas pada jarak (a) 40 cm dan (b) 25 cm
Pembahasan
(a) Data yang diperoleh dari soal adalah $S_{n}$ = 2 meter = 200 cm dan $s$ = 0,4 meter = 40 cm. Dengan menggunakan persamaan untuk mata rabun dekat diperoleh \[f_{lensa}=\frac{S_{n}s}{S_{n}-s}=\frac{(200)(40)}{(200)-(40)}=50\,cm\]
\[P_{lensa}=\frac{100}{f}=\frac{100}{50}=2\,\,Dioptri\]
atau menggunakan cara tanpa mencari $f$ \[P_{lensa}=\frac{1}{s}-\frac{1}{s_{n}}=\frac{1}{0,40}-\frac{1}{2}=2,5-0,5=2\,\,Dioptri\]
Titik dekat seseorang yang rabun dekat adalah 2 meter. Tentukanlah kuat lensa kacamata yang diperlukan jika orang tersebut ingin membaca dengan jelas pada jarak (a) 40 cm dan (b) 25 cm
Pembahasan
(a) Data yang diperoleh dari soal adalah $S_{n}$ = 2 meter = 200 cm dan $s$ = 0,4 meter = 40 cm. Dengan menggunakan persamaan untuk mata rabun dekat diperoleh \[f_{lensa}=\frac{S_{n}s}{S_{n}-s}=\frac{(200)(40)}{(200)-(40)}=50\,cm\]
\[P_{lensa}=\frac{100}{f}=\frac{100}{50}=2\,\,Dioptri\]
atau menggunakan cara tanpa mencari $f$ \[P_{lensa}=\frac{1}{s}-\frac{1}{s_{n}}=\frac{1}{0,40}-\frac{1}{2}=2,5-0,5=2\,\,Dioptri\]
(b) Untuk melihat benda pada jarak 25 cm = 0,25 m, kuat lensa dihitung menggunakan persamaan terakhir poin (a) \[P_{lensa}=\frac{1}{s}-\frac{1}{s_{n}}=\frac{1}{0,25}-\frac{1}{2}=2,5-0,5=3,5\,\,Dioptri\]
atau cara langsung \[P_{lensa}=4-\frac{1}{s_{n}}=4-\frac{1}{2}=3,5\,\,Dioptri\]
atau cara langsung \[P_{lensa}=4-\frac{1}{s_{n}}=4-\frac{1}{2}=3,5\,\,Dioptri\]
Perbesaran anguler (sudut) oleh lup untuk keadaan mata berakomodasi maksimum adalah \[M_{a}=\frac{s_{n}}{f}+1\]
Perbesaran anguler (sudut) oleh lup untuk keadaan mata tak berakomodasi adalah \[M_{a}=\frac{s_{n}}{f}\]
MikroskopPerbesaran anguler lup ternyata memiliki batas maksimum. Jika $f$ diperkecil terus untuk memperoleh perbesaran anguler yang lebih besar akan teradi cacat bayangan sehingga bayangan menjadi kabur. Mikroskop dapat digunakan lebih baik daripada lup, yaitu untuk melihat benda-benda yang jauh lebih kecil tanpa cacat bayangan. Bayangan akhir yang dibentuk oleh mikroskop bersifat diperbesar, maya, terbalik.
Beberapa ciri-ciri mikroskop:
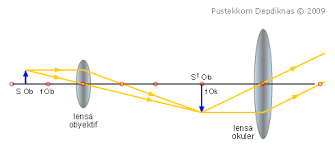
- memiliki dua lensa positif, yaitu lensa objektif dan lesa okuler
- lensa objektif terletak dekat benda (objek) dan lensa okuler terletak dekat mata, lensa okuler sebagai lup dan dapat digeser-geser
- jarak fokus lensa objektif lebih kecil dari jarak fokus lensa okuler
- benda yang akan diamati diletakkan di Ruang II benda dari lensa objektif. ($f_{ob}$ < $s_{ob}$ $2f_{ob}$ )
Perbesaran oleh lensa objektif, \[M_{ob}=\frac{h'_{ob}}{h_{ob}}=\frac{s'_{ob}}{s_{ob}}=\frac{f_{ob}}{s_{ob}-f_{ob}}\]
Perbesaran oleh lensa okuler sama persis dengan perbesaran oleh lup yaitu
Perbesaran total oleh mikroskop adalah hasil kali perbesaran oleh lensa objektif dan lensa okuler \[M_{total}=M_{ob}\times M_{ok}\]- untuk keadaan mata berakomodasi maksimum adalah \[M_{a}=\frac{s_{n}}{f_{ok}}+1\]
- untuk keadaan mata tak berakomodasi adalah \[M_{a}=\frac{s_{n}}{f_{ok}}\]
Contoh soal dan pembahasan Mikroskop
Sebuah benda diletakkan 6 cm di bawah mikroskop yang mempunyai panjang fokus lensa objektif 4 cm dan panjang fokus lensa okuler 10 cm. Perbesaran bayangan yang terlihat jika mata melihat dengan (a) akomodasi maksimum, dan (b) tanpa akomodasi!
Pembahasan
Diketahui $s_{ob}$ = 6 cm, $f_{ob}$ = 4 cm, $f_{ok}$ = 16 cm, $s_{n}$ = 25 cm, maka
(a) Mata berakomodasi maksimum \[M_{total}=M_{ob}\times M_{ok}=\frac{f_{ob}}{s_{ob}-f_{ob}}\times \frac{s_{n}}{f_{ok}}+1=\frac{4}{6-4}\times \left (\frac{25}{10}+1 \right )=7\,kali\]
(b) Mata tidak berakomodasi \[M_{total}=M_{ob}\times M_{ok}=\frac{f_{ob}}{s_{ob}-f_{ob}}\times \frac{s_{n}}{f_{ok}}=\frac{4}{6-4}\times \frac{25}{10}=5\,kali\]
Teropong Bumi
Teropong bumi ayng disebut juga sebagai teropong medan atau teropong yojana menghasilkan bayangan akhir yang tegak terhadap arah benda semula. Hal ini dapat diperoleh dengan menggunakan lensa cembung ketiga yang disisipkan di antara lensa objektif dan lensa okuler. Lensa cembung ketiga hanya berfungsi membalik bayangan tanpa perbesaran. Oleh karena itu disebut juga sebagai lensa pembalik.
Panjang teropong bumi untuk mata tidak berakomodasi adalah \[d=f_{objektif}+4f_{pembalik}+f_{okuler}\]
Referensi [2]Teropong bumi ayng disebut juga sebagai teropong medan atau teropong yojana menghasilkan bayangan akhir yang tegak terhadap arah benda semula. Hal ini dapat diperoleh dengan menggunakan lensa cembung ketiga yang disisipkan di antara lensa objektif dan lensa okuler. Lensa cembung ketiga hanya berfungsi membalik bayangan tanpa perbesaran. Oleh karena itu disebut juga sebagai lensa pembalik.
Panjang teropong bumi untuk mata tidak berakomodasi adalah \[d=f_{objektif}+4f_{pembalik}+f_{okuler}\]
Terima kasih sudah ke sini untuk membaca dan belajar fisika. Jangan ragu untuk menyukai posting blog, berlangganan blog dan berkomentar untuk berinteraksi lebih dengan saya. Selamat belajar ya. Thank you for coming here to read and study physics in this blog. Feel free to like, subscribe and comment. Have a nice learning.
By
Label: Optik
Label: Optik
