Pada pembahasan kali ini, kita akan mencoba memahami konsep medan magnetik dengan pendekatan kuantitatif, atau sederhananya pendekatan dengan angka-angka/perhitungan matematis.
Persamaan / formula mengenai medan magnetik kita turunkan secara matematik menggunakan hitung dasar integral, termasuk juga perkalian silang antara dua vektor.
Hukum Biot - Savart sebagai Follow Up Penemuan Oersted
Ternyata magnet dan listrik memiliki hubungan yang dalam bahasa sederhananya, dengan adanya magnet kita bisa membuat listrik. Begitu sebaliknya dengan adanay listrik kita bisa membuat magnet.
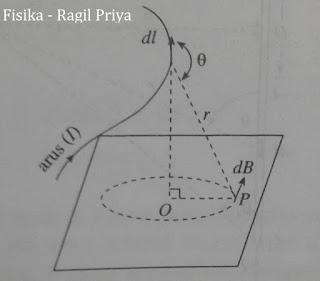 |
| Elemen penghantar dl berarus I menimbulkan induksi magnetik dB di titik P yang berjarak r dari dl |
Nah, lebih tepatnya pertama kali teramati oleh fisikawan Denmark yaitu H.C. Oersted awal 1800 -an. Percobaanya membuktikan bahwa kalau ada arus listrik (muatan yang mengalir) pada kabel menyebabkan berbeloknya jarum kompas di sekitar kabel berarus tersebut.
Fenomena berbeloknya jarum kompas tersebut menunjukkan bahwa arus listrik menyebabkan medan magnet.
Kemudian penemuan Oersted ini ditindaklanjuti oleh dua fisikawan Perancis yaitu Jean Baptise Biot dan Felix Savart. Keduanya mampu menemukan hal baru lebih lanjut mengenai medan magnet oleh arus listrik. Pemenuannya yaitu berhasil menentukan bentuk medan magnet yang ditimbulkan oleh arus listrik yang stabil.
Kedua ilmuan Perancis ini berhasil mengamati kontribusi elemen / bagian kecil induksi megnetik $dB$ pada suatu titik $P$ yang ditimbulkan oleh elemen penghantar dl yang dialiri arus listrik I.
Perhatikan gambar di atas.
Kesimpulan yang diperoleh Biot – Savart secara geometri dari gambar tersebut mengenai besar induksi magnetik adalah :
- Sebanding dengan panjang elemen penghantar $dl$
- Sebanding dengan kuat arus listrik $I$
- Sebanding dengan nilai sinus dari sudut apit tetha antara arah arus pada dl dengan garis penghubung titik $P$ dengan $dl$
- Berbanding terbalik dengan kaudrat jarak $r$ antara titik $P$ dengan elemen penghantar $dl$
Persamaan matematis yang diperoleh yaitu:
\[dB=k\frac{Idlsin\theta }{r^{^{2}}}\]
dengan $k$ = sebuah tetapan yang memenuhi hubungan
\[k=\frac{\mu _{0}}{4\pi }\]
Maka dengan subtitusi nila $k$ ini ke persamaan pertama di atas, menjadi
\[dB=\frac{\mu _{0}}{4\pi }\frac{Idlsin\theta }{r^{2}}\]
dengn $\mu _{0}$ adalah permeabilitas vakum, $4\pi x\,10^{-7}\frac{Wb}{m.A}$
Rumusan Hukum Biot – Savart adalah rumusan umum mengenai kuat medan magnet di sekitar kawat berarus listrik, apa pun bentuk konduktornya tersebut.
Nah kali ini kita akan membahas mengenai kuat medan magnet untuk beberapa bentuk penghantar.
Ada empat hal yang akan kita bahas secara khusus. Pertama yang konduktornya berupa kawat lurus. Kedua kawat konduktor yang bentuknya melingkar. Ke tiga berupa solenoida. Dan terakhir berupa toroida.
Baca juga Soal Jawab Hukum Ohm
Kaidah Tangan Kanan untuk Menentukan Arah Medan Magnetik
Sebagai gambaran hubungan antara arah arus listrik dan arah medan magnetik, kita pakai kaidah tangan kanan.
Perhatikan gambar berikut ini
 |
| Kaidah tangan kanan. Induksi Magnetik B yang ditimbulkan oleh penghantar lurus berarus listrik |
Rumusan Hukum Biot – Savart adalah rumusan umum mengenai kuat medan magnet di sekitar kawat berarus listrik, apa pun bentuk konduktornya tersebut.
Nah kali ini kita akan membahas mengenai kuat medan magnet untuk beberapa bentuk penghantar.
Ada empat hal yang akan kita bahas secara khusus. Pertama yang konduktornya berupa kawat lurus. Kedua kawat konduktor yang bentuknya melingkar. Ke tiga berupa solenoida. Dan terakhir berupa toroida.
Baca juga Arus, Tegangan, Hambatan Listrik
Induksi Magnetik di Sekitar Kawat Penghantar Lurus Berarus Listrik
Kuat medan magnet $B$ yang ditimbulkan oleh kawat penghantar lurus berarus listrik $I$ pada tempat sekitar kawat tersebut yang berjarak $a$ adalah sebagai berikut.\[\displaystyle \LARGE B=\frac{\mu_{0}\,I}{2\pi\,a}\]
Secara matematis persamaan ini diperoleh dari penyelesaian integral persamaan dasar Huum Biot - Savart.
Mari kita bahas penurunan rumusnya dengan menyimak gambaran penerapan hukum Biot - Savart pada penghantar berarus listrik berikut ini.
Dari gambar tampak bahwa :
\[sin\, \theta =\frac{a}{r}\rightarrow r=\frac{a}{sin\, \theta }=a\,cosec\,\theta\]
Nah, ketiga hubungan ini bila kita subtitusikan ke persamaan Hukum Biot - Savart, $\displaystyle dB=\frac{\mu _{0}}{4\pi }\frac{I\,dl\,sin\theta }{r^{2}}$ , maka akan diperoleh:
\[dB=\frac{\mu_{0}}{4\pi}\frac{I\,dl\,sin\,\theta}{r^{2}}\]
Mari kita bahas penurunan rumusnya dengan menyimak gambaran penerapan hukum Biot - Savart pada penghantar berarus listrik berikut ini.
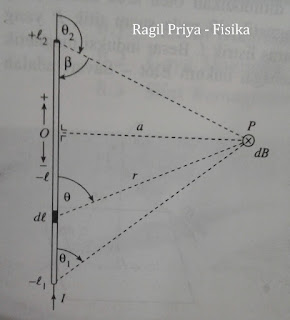 |
| Penerapan hukum Biot - Savart pada penghantar berarus listrik |
Dari gambar tampak bahwa :
\[sin\, \theta =\frac{a}{r}\rightarrow r=\frac{a}{sin\, \theta }=a\,cosec\,\theta\]
\[cotan\,\theta =\frac{-l}{a}\rightarrow l=(-a)\,cotan\,\theta\]
\[dl=a\,cosec^{2}\theta \,d\theta\]
\[dB=\frac{\mu_{0}}{4\pi}\frac{I\,dl\,sin\,\theta}{r^{2}}\]
\[dB=\frac{\mu_{0}}{4\pi}\frac{I\,(a\,cosec^{2}\,\theta\,d\,\theta)\,sin\,\theta}{a^{2}\,cosec^{2}\,\theta}\]
\[dB=\frac{\mu_{0}}{4\pi}\frac{I\,sin\,\theta\,d\,\theta}{a}\]
Kemudian nilai $B$ kita tentukan dengan metode integral sebagai berikut ini:
$\displaystyle B=\int_{\theta_{1}}^{\theta_{2}}dB$
$\displaystyle B=\int_{\theta_{1}}^{\theta_{2}}\frac{\mu_{0}}{4\pi}\frac{I\,sin\,\theta\,d\,\theta}{a}$
$\displaystyle B=\frac{\mu_{0}\,I}{4\pi\,a}\int_{\theta_{1}}^{\theta_{2}}sin\,\theta\,d\,\theta$
$\displaystyle B=\frac{\mu_{0}\,I}{4\pi\,a}(-cos\,\theta)\mid_{\theta_{1}}^{\theta_{2}}$
$\displaystyle B=\frac{\mu_{0}\,I}{4\pi\,a}(cos\,\theta_{2}-cos\,\theta_{1})$
Jadi diperoleh \[\displaystyle \LARGE B=\frac{\mu_{0}\,I}{4\pi\,a}(cos\,\theta_{2}-cos\,\theta_{1})\]
Selanjutnya, oleh karena $\displaystyle \theta_{2}+\beta=180^{\circ}$ , maka $\displaystyle cos\,\theta_{2}=-\,cos\,\beta$
Kemudian untuk menyederhanakan notasi, kita nyatakan $\displaystyle \theta_{1}=\alpha$
Dengan demikian, persamaannya dapat ditulis ulang menjadi
\[\displaystyle \LARGE B=\frac{\mu_{0}\,I}{4\pi\,a}(cos\,\alpha+cos\,\beta)\]
Apabila kawat penghantarnya sangat panjang, maka sudut $\displaystyle \alpha=0^{\circ}$ dan $\displaystyle \beta=0^{\circ}$. Oleh karena itu
$\displaystyle B=\frac{\mu_{0}\,I}{4\pi\,a}(cos\,0^{\circ}+cos\,0^{\circ})$
$\displaystyle B=\frac{\mu_{0}\,I}{4\pi\,a}(1+1)$
Diperoleh \[\displaystyle \LARGE B=\frac{\mu_{0}\,I}{2\pi\,a}\]
Bersambung
$\displaystyle B=\int_{\theta_{1}}^{\theta_{2}}\frac{\mu_{0}}{4\pi}\frac{I\,sin\,\theta\,d\,\theta}{a}$
$\displaystyle B=\frac{\mu_{0}\,I}{4\pi\,a}\int_{\theta_{1}}^{\theta_{2}}sin\,\theta\,d\,\theta$
$\displaystyle B=\frac{\mu_{0}\,I}{4\pi\,a}(-cos\,\theta)\mid_{\theta_{1}}^{\theta_{2}}$
$\displaystyle B=\frac{\mu_{0}\,I}{4\pi\,a}(cos\,\theta_{2}-cos\,\theta_{1})$
Jadi diperoleh \[\displaystyle \LARGE B=\frac{\mu_{0}\,I}{4\pi\,a}(cos\,\theta_{2}-cos\,\theta_{1})\]
Selanjutnya, oleh karena $\displaystyle \theta_{2}+\beta=180^{\circ}$ , maka $\displaystyle cos\,\theta_{2}=-\,cos\,\beta$
Kemudian untuk menyederhanakan notasi, kita nyatakan $\displaystyle \theta_{1}=\alpha$
Dengan demikian, persamaannya dapat ditulis ulang menjadi
\[\displaystyle \LARGE B=\frac{\mu_{0}\,I}{4\pi\,a}(cos\,\alpha+cos\,\beta)\]
Apabila kawat penghantarnya sangat panjang, maka sudut $\displaystyle \alpha=0^{\circ}$ dan $\displaystyle \beta=0^{\circ}$. Oleh karena itu
$\displaystyle B=\frac{\mu_{0}\,I}{4\pi\,a}(cos\,0^{\circ}+cos\,0^{\circ})$
$\displaystyle B=\frac{\mu_{0}\,I}{4\pi\,a}(1+1)$
Diperoleh \[\displaystyle \LARGE B=\frac{\mu_{0}\,I}{2\pi\,a}\]
Bersambung
